Kiedy szczyt epidemii koronawirusa? „Za około 10 dni”
SANOK / RZESZÓW / PODKARPACIE. Otrzymaliśmy wyniki badań jednego z naukowców Wyższej Szkoły Informatyki i Zarządzania w Rzeszowie. Dr Andrew Schumann stworzył model przebiegu epidemii w Polsce i na podstawie globalnych danych pokusił się o wyznaczenie prawdopodobnego szczytu zachorowań w naszym kraju, a jednocześnie okresu, w którym powinniśmy odnotowywać stały spadek liczby kolejnych zakażonych osób.
Lektura dotycząca opracowania dr Andrew Schumanna jest dosyć obszerna i pisana fragmentami specjalistycznym językiem. Dla mniej cierpliwych przedstawiamy najważniejsze informacje z raportu, który otrzymaliśmy z Wyższej Szkoły Informatyki i Zarządzania w Rzeszowie.
Kiedy nastąpi szczyt zachorowań na COVID-19?
- W mediach pojawiło się już wiele spekulacji na temat tego, kiedy mamy spodziewać się szczytu epidemii Covid-19 oraz wejścia krzywej zachorowań w strefę plateau – czyli wypłaszczenia. W tych spekulacjach pojawia się jednak sporo błędów, a tymczasem, korzystając z globalnych danych umieszczonych na stronie: https://www.worldometers.info/coronavirus/ możemy dość precyzyjnie obliczyć moment szczytu zachorowań dla każdego kraju.
- Metoda zastosowania przez dr Schumanna opiera się na relacji aktywnych zachorowań do tzw. zamkniętych przypadków (osób wyleczonych i zmarłych).
- Za szczyt zachorowań uważa się moment, w którym liczba chorujących równa się liczbie zamkniętych przypadków. Prościej mówiąc, jest to dzień, kiedy liczba wszystkich osób nadal jeszcze chorujących równa się połowie wszystkich osób zarejestrowanych.
- Na dzień 5 maja, w Polsce mieliśmy 14 431 odnotowanych zachorowań, 4280 wyzdrowień i 716 zgonów.
-
Bazując na modelu zastosowanym przez naukowca z rzeszowskiej uczelni, Polska odnotuje szczyt zachorowań za około 10 dni.
SZCZEGÓŁOWY RAPORT
 Dr Andrew Schumann, prof. WSIiZ
Dr Andrew Schumann, prof. WSIiZ
Kierownik Katedry Kognitywistyki i Modelowania Matematycznego Wyższej Szkoły Informatyki i Zarządzania w Rzeszowie. Specjalista w zakresie logiki, kognitywistyki i sztucznej inteligencji. Uczestniczył m.in. w opracowaniu prototypu biologicznego komputera, stworzonego na podstawie zachowania się wielojądrowego jednokomórkowego organizmu Physarum polycephalum (projekt koordynował Uniwersytet Zachodniej Anglii w Bristolu). Ostatnio pracował nad modelowaniem zachowania się różnych typów roju – m.in. społecznych bakterii, pszczół i mrówek. Lubi sztuki wizualne: malarstwo, rysunek i fotografię.
W mediach pojawiło się już wiele spekulacji na temat tego, kiedy mamy spodziewać się szczytu epidemii Covid-19 oraz wejścia krzywej zachorowań w strefę plateau – czyli wypłaszczenia. W tych spekulacjach pojawia się jednak sporo błędów, a tymczasem, korzystając z globalnych danych umieszczonych na stronie: https://www.worldometers.info/coronavirus/ możemy dość precyzyjnie obliczyć moment szczytu zachorowań dla każdego kraju.
Bazowe parametry dla dowolnej epidemii:
x(i) – nowe wypadki na dzień i; każdego dnia ich liczba wzrasta, konkretnego dnia osiąga maksimum, po czym następuje spadek. Na podanej stronie jest to kolumna New cases;
X(i) = Sum x(i) – to suma wszystkich przypadków zachorowań do dnia i. Ten parametr tylko rośnie, dochodzi do maksimum i zaprzestaje wzrostu (dzieje się tak, jeśli w ogóle nie przybywa już nowych przypadków). Na stronie jest to kolumna Total cases;
c(i) – zakończone (zamknięte) przypadki na dzień i, czyli liczba osób, które zmarły albo są wyleczone na ten dzień. Liczby c(i) rosną każdego dnia, pewnego dnia osiągają maksimum i następnie maleją. Na wskazanej stronie tej kolumny nie ma;
C(i) = Sum c(i) – to suma wszystkich zamkniętych wypadków do dnia i. Ten parametr tylko rośnie i dochodzi do maksimum. Po osiągnięciu maksimum suma ta spowalnia swój wzrost, a przestaje rosnąć tylko wtedy, gdy już nie ma nowych zgonów ani też nie przybywa osób wyleczonych: co oznacza, że epidemia ustaje. Na stronie jest to suma kolumn Total deaths i Total recovered;
A (i) = X(i) – C(i) – aktywne wypadki na dzień i: to liczba tych osób, które pozostają chore (nie znajdują się w grupie osób wyleczonych ani zmarłych). Na stronie jest to kolumna Active cases.
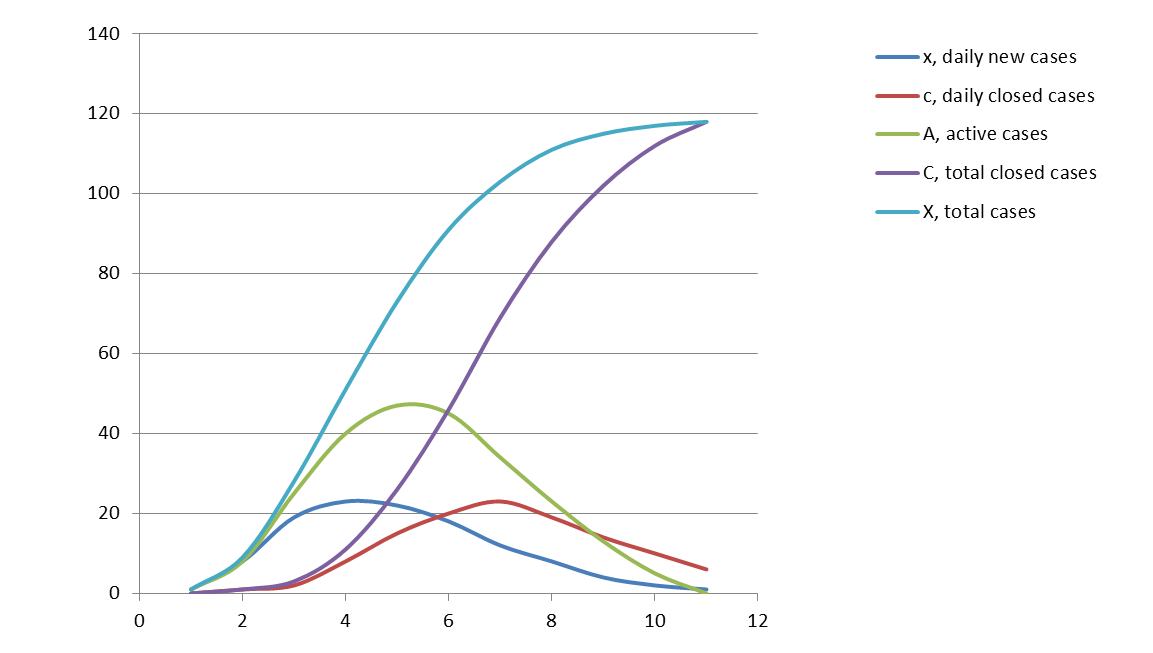
Wszystkie te parametry można w łatwy sposób przedstawić graficznie. Z podstaw epidemiologii wiemy, że idealny wykres dla nowych wypadków (x) każdej epidemii jest to krzywa lognormalna. Krzywa dla zakończonych przypadków (c) przebiega podobnie do krzywej dla nowych przypadków (x) z przesunięciem odpowiadającym opóźnieniu o tę liczbę dni, które są konieczne, aby każdy nowy wypadek został zamknięty. Zachowanie się krzywej dla zamkniętych przypadków (c) zależy w ten sposób tylko od dwóch czynników – od przebiegu krzywej nowych przypadków (x) i od tego, jak szybko zamyka się każdy nowy przypadek. Krzywa aktywnych wypadków (A) też jest lognormalna i jej przebieg odpowiada przebiegowi krzywej nowych przypadków – ale z większą amplitudą. Im więcej dni potrzeba na zamknięcie przypadków z przeszłości, tym więcej przypadków się nawarstwia i amplituda będzie większa.
Spróbujmy zbudować idealny wykres przebiegu epidemii z parametrami x(i), X(i), c(i), C(i), A(i); przy czym na osi y zaznaczamy liczbę zakażonych, a na osi x liczbę dni, w których epidemia rozwija się i wygasa.
W ten sposób epidemia rozwija się początkowo eksponencjalnie (ma przebieg taki, jak np. wykres funkcji ex) i osiąga maksimum nowych wypadków dziennych (x). Po pewnym czasie zostaje też osiągnięty szczyt aktywnych wypadków dziennych (A), a w końcu wszystkie przypadki zakażenia (X) osiągają plateau – epidemia ustaje, nie przybywa nowych przypadków. Zatem mamy dwa szczyty epidemii i jedno plateau. Pierwszy szczyt to maksimum nowych przypadków dziennych, drugi to maksimum w liczbie dziennych aktywnych przypadków. Po osiągnięciu maksimum aktywnych przypadków epidemia wkrótce wychodzi na plateau i przestaje być niebezpieczna.
Naszym zadaniem jest nauczyć się prognozować dzień szczytu aktywnych przypadków (A) bez złożonych obliczeń. Temu szczytowi w przybliżeniu odpowiada przecięcie dwóch krzywych: nowych wypadków (x) i zamkniętych wypadków (c) na dzień i. Problem jest taki, że nowe wypadki (x) i zamknięte wypadki (c) mają duże wahania przypadkowe i dlatego dynamikę x oraz c trudno jest prognozować dokładnie.
Za szczyt aktywnych wypadków (A) z krótkim opóźnieniem tj. 4 – 10 dni, odpowiada część, bliska 50%, aktywnych wypadków (A) w stosunku do wszystkich wypadków zakażenia (X). W tym punkcie właśnie mamy przecięcie A(i) i C(i). Oznacza to, że w tym dniu liczba chorujących równa się liczbie zamkniętych przypadków (osób wyleczonych i zmarłych), czyli A(i) = C(i). Prościej mówiąc, jest to dzień, kiedy liczba wszystkich osób nadal jeszcze chorujących równa się połowie wszystkich osób zarejestrowanych.
Oznacza to, że przebieg epidemii możemy rozumieć w następujący sposób. Bierzemy zamknięte przypadki na dzisiaj (C(i) – różnica kolumn Total cases i Active cases). Dzielimy je przez liczbę wszystkich przypadków (X(i) – kolumna Total cases). Mnożymy przez 100. Otrzymujemy część zamkniętych przypadków w stosunku do wszystkich przypadków w procentach. Porównujemy tę część z 50%. Jeśli wynosi ona poniżej 20%, to epidemia jeszcze jest na początku zachorowań na starcie i szczyt zachorowań jeszcze nie nastąpił. Jeśli ten stosunek jest większy niż 50%, to epidemia na pewno swój szczyt już przeszła i szybko się zakończy. Przy końcu epidemii wszystkie zamknięte przypadki na dzisiaj równe są sumie wszystkich przypadków zakażenia (C(i) = X(i)).
Jak to zastosować na praktyce? Wiadomo, że w Polsce jest (według danych z 5-go maja 2020r.), 14431 osób z pozytywnym wynikiem testu na infekcję COVID-19, 4280 osób wyzdrowiało, natomiast 716 pacjentów z koronawirusem zmarło. Czyli X = 14431 (przypomnimy, że jest to suma wszystkich wypadków zakażenia), C = 4996 (to suma wszystkich zamkniętych przypadków, czyli wszystkich osób, które zmarły bądź zostały wyleczone). Teraz liczbę zamkniętych przypadków, czyli 4996, dzielimy przez 14431, a potem mnożymy przez 100. Daje to 34,62 % zamkniętych przypadków. Z poprzednich ustaleń wiemy, że szczyt epidemii (aktywnych wypadków) na pewno minął, jeśli ten stosunek byłby 50%. Czyli w Polsce do przecięcia A(i) i C(i) brakuje jeszcze 15,38 % a to zajmie około 10 dni według prognozy naiwnej (kiedy przedłużamy istniejący wykres C(i)). Wynika z tego, że w przybliżeniu już znajdujemy się mniej więcej w szczycie zachorowań A(i). W ciągu tygodnia musi zacząć się spadek zachorowań według prognozy naiwnej.
Inne przykłady:
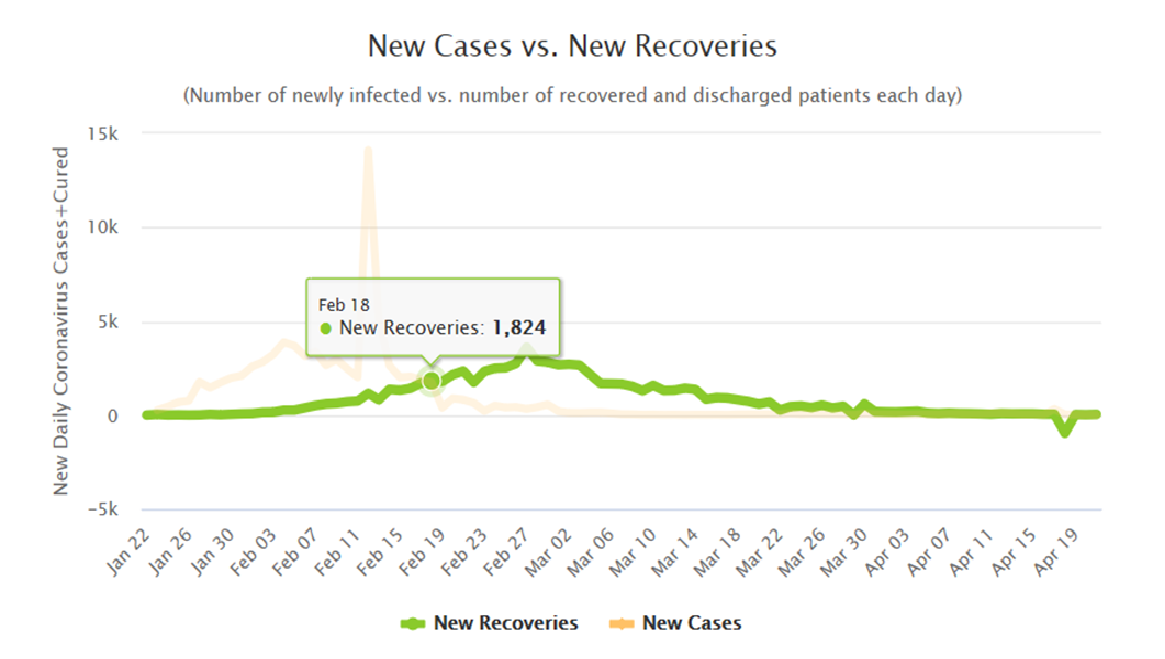
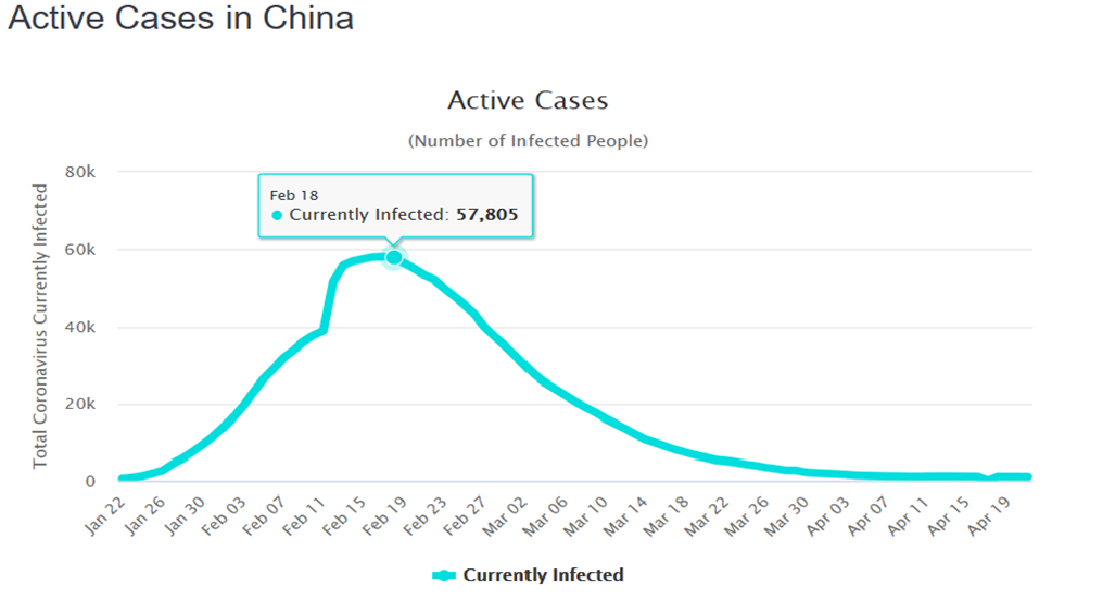
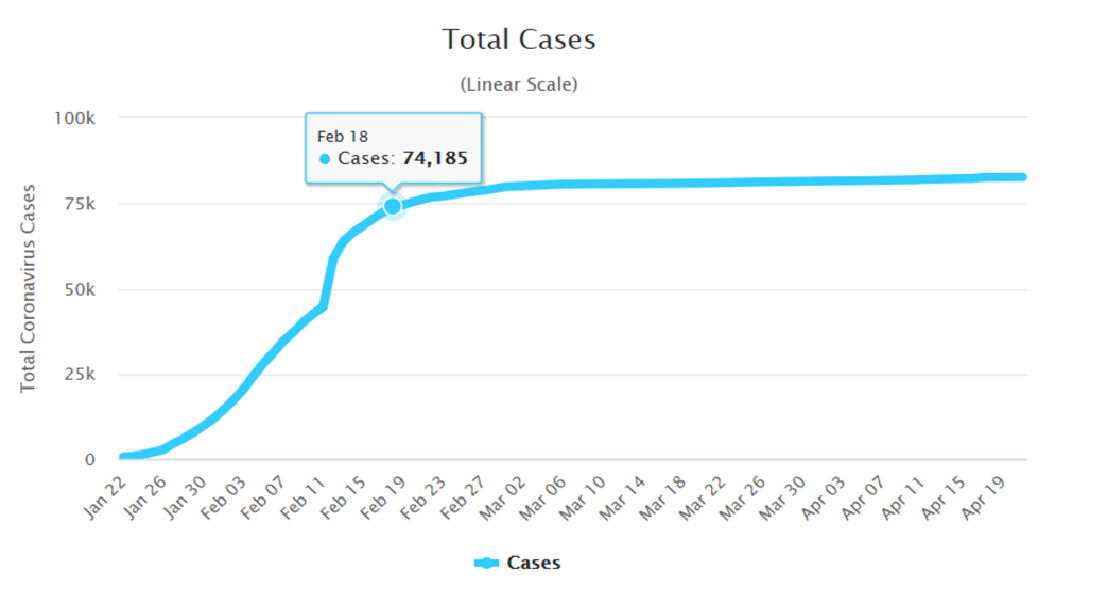
Chiny – Przecięcie x(i) i c(i) nastąpiło w Chinach 18 lutego (wszystkie następne rysunki – skreenshoty z podanej strony).
W ten sam dzień obserwujemy szczyt aktywnych wypadków A(i):
W tym dniu wszystkie przypadki X(i) weszły w obszar plateau.
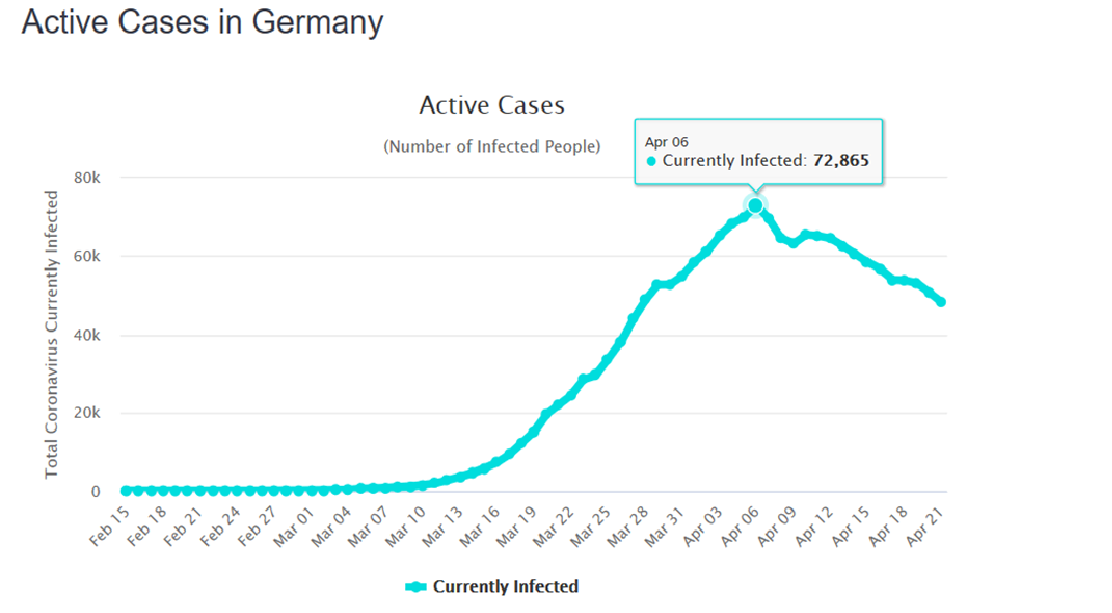
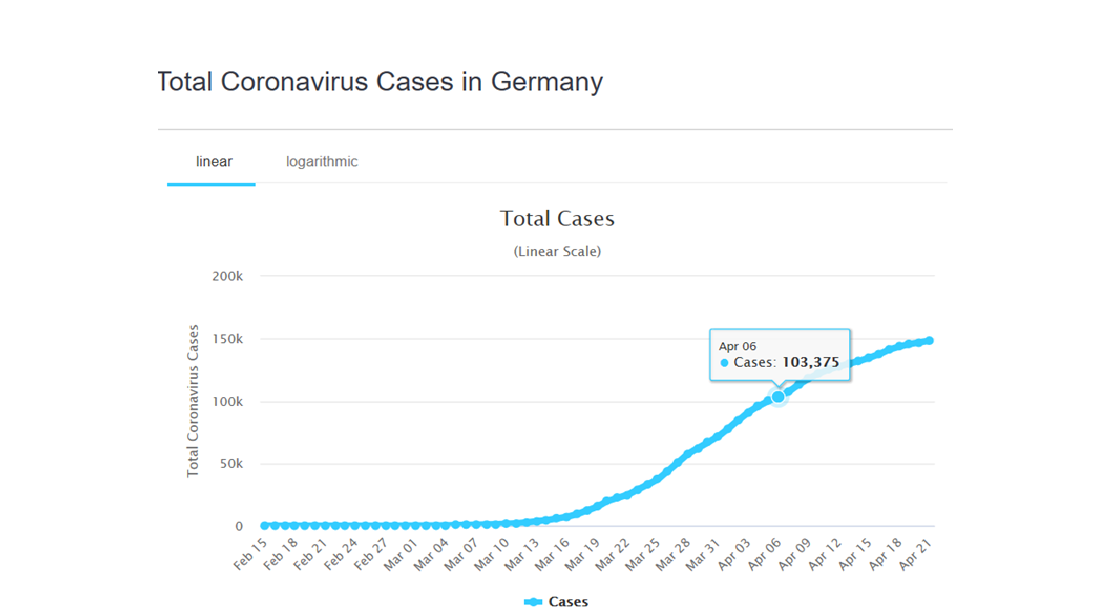
Niemcy
Przecięcie x(i) i c(i) nastąpiło 7 kwietnia.
Prawie w ten sam dzień obserwujemy szczyt aktywnych wypadków A(i):
I w tym dniu wszystkie przypadki X(i) zbliżyły się do obszaru plateau:
źródło: Red., Wyższa Szkoła Informatyki i Zarządzania w Rzeszowie


 Wykop.pl
Wykop.pl
























Dodaj komentarz
Zaloguj się a:
- Twój komentarz zostanie wyróżniony,
- otrzymasz punkty, które będziesz mógł wymienić na nagrody,
- czytelnicy będa mogli oceniać Twoją wypowiedź (łapki),
lub dodaj zwykły komentarz, który zostanie wyświetlany na końcu strony, bez możliwosci głosowania oraz pisania odpowiedzi.Dodając komentarz akceptujesz postanowienia regulaminu.